• Random Vibration con FEMAP

Análisis Dinámico de Vibraciones Aleatorias (Random) con Simcenter FEMAP y Simcenter Nastran

Hay casos donde la excitación dinámica de una estructura no se puede definir de forma precisa: por ejemplo, un avión en vuelo atravesando una turbulencia de aire soportará cargas dinámicas, pero debido a la naturaleza de la turbulencia esas cargas serán diferentes si un segundo avión de idénticas características atraviesa la misma turbulencia en otro instante de tiempo. A pesar de que la variación frente al tiempo de ambas cargas no es idéntica, sin embargo tienen las mismas características y se puede obtener una estimación de la respuesta dinámica en ambos aviones.

El Análisis de Respuesta Aleatoria (Random Frequency Response Dynamic Analysis) es un tipo de análisis dinámico que sólo se puede describir en sentido estadístico, no determinista y tiene las siguientes características:

• Es estacionario: significa que la media estadística del proceso no cambian con el tiempo, es decir, la relación entre X(t1) y X(t2) dependen sólo de t1-t2, no del valor de t1 y t2.
• Es ergódico: significa que la media en el tiempo total es estadísticamente equivalente a la media de los sucesos encadenados, es decir, un conjunto de sucesos ensamblados en el tiempo tendrán el mismo efecto estadístico que un único suceso partido en trozos.
• En resumen: la magnitud instantánea de la vibración no se conoce en un instante dado, pero se puede expresar en términos de sus propiedades estadísticas tales como su valor medio, la desviación standard, y la probabilidad de exceder un cierto valor.

En el mundo real las vibraciones aleatorias se producen por todas partes: terremotos, tsunamis, fluctuaciones de la presión del viento (turbulencias) en aviones y edificaciones de altura elevada, excitación acústica debido al ruido en cohetes y motores a reacción, vibración en coches, aviones, etc…

• En Simcenter Nastran el Análisis RANDOM es un postprocesado del Análisis Dinámico de Respuesta en Frecuencia (SOL111).
• Mientras que un análisis harmónico de barrido en frecuencia (SOL111) excita las frecuencias una a una, un análisis de vibraciones aleatorias excita todas las frecuencias de golpe (es como pulsar todas las teclas de un piano a la vez), por tanto la respuesta en un análisis RANDOM será peor a nivel estructural que la obtenida mediante un análisis de barrido en frecuencia (sine frequency swept).
• Uno de lo principales objetivos del análisis RANDOM en la industria es buscar los límites del diseño, el fallo del equipo o componente a ensayar. Por ejemplo, a un fabricante le gustaría saber si un producto falla a diferentes niveles de vibración del entorno, lo que le permitiría conocer las debilidades del producto y la forma de mejorarlo.
• Un análisis RANDOM es mucho más realista que un análisis de barrido en frecuencia (SOL111) porque el análisis RANDOM “simultáneamente excita todas las frecuencias de resonancia” de la estructura. En un SOL111 se puede encontrar una frecuencias de resonancia en una parte de la estructura y resonar a otra frecuencia en otra parte del equipo. Encontrar frecuencias de resonancia separadas en diferente momento puede no causar el fallo, pero cuando todas las frecuencias de resonancia se excitan al mismo tiempo, es la situación más severa.

La intensidad de la excitación RANDOM se define en el dominio de la frecuencia mediante una función denominada Densidad Espectral de Potencia (Power Spectral Density, PSD) que se crea sometiendo a la estructura a una vibración de ruido blanco, midiendo la amplitud de la respuesta RMS en todo el rango de la frecuencia, elevando al cuadrado la respuesta, y dividiendo por el rango de la frecuencia, resultando en unidades G²/Hz, donde G = a/g = aceleración/gravedad, por tanto G no tiene unidades. Un PSD con una aceleración de 10G significa que la aceleración tiene una magnitud que es 10 veces mayor que la aceleración de la gravedad. Realmente la función se define como una Densidad Espectral de Aceleración (Acceleration Spectral Density, ASD) pero se sigue denominando PSD, aunque el término ASD sería el más apropiado cuando se usa la aceleración para definir la excitación.

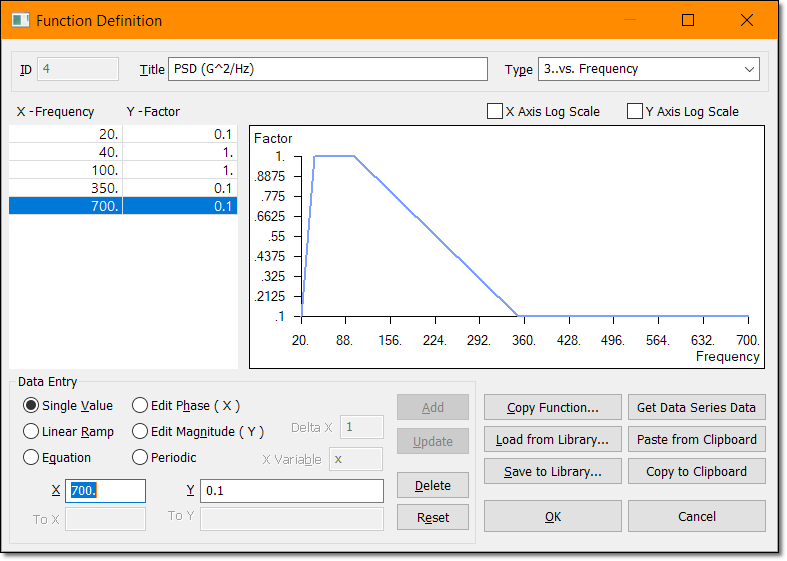
La siguiente imagen muestra una excitación típica PSD para un Análisis Random Vibration (aclarar que esta gráfica PSD no será la excitación PSD que utilizaremos en el ejemplo propuesto):

   

Un sistema sujeto a vibraciones aleatorias no tiene una única tensión resultante. Afortunadamente para nosotros, los resultados de tensión siguen una distribución en forma de campana de Gauss.

La distribución mediante campana de Gauss permite presentar las tensiones en formato estadístico. La tensión RMS que vemos en Simcenter FEMAP tras un análisis RANDOM corresponde a la tensión 1σ.

• La tensión 1σ representa la tensión que sufre la estructura el 68.3% del tiempo.
• La tensión 2σ = 2 * 1σ se produce el 95.4 – 68.3 = 27.1% del tiempo.
• La tensión 3σ = 3 * 1σ se da en el 99.7 – 95.4 = 4.3% del tiempo.
• La tensión 4σ = 4 * 1σ sólo pasará el 100 – 99.7 = 0.3% del tiempo.
• La mayor parte de las veces un equipo o componente estructural se diseña para que sea capaz de soportar un nivel de tensión 3σ todo el tiempo.

Ejemplo: HINGE

Vamos a utilizar el ejemplo de FEMAP que viene en la lista de problemas en HELP > EXAMPLES para aprender a realizar un Análisis Random de vibraciones aleatorias excitada en la dirección del eje Z por una densidad espectral de aceleración (ASD) en unidades G^2/Hz, usando un amortiguamiento crítico del 10% constante en el rango de frecuencia.

El modelo está en unidades americanas (psi, in, snails), así que lo hemos convertido al sistema internacional (MPa, mm, Tons) usando la orden TOOLS > CONVERT UNITS, aprovechando para redondear las dimensiones a valores enteros, sin decimales. Se trata de estudiar la respuesta dinámica a un análisis RANDOM de una pieza de acero de espesor 6 mm de material S335JR.

Particionando la geometría en regiones regulares se llega a conseguir una calidad de la malla elevada con la menor distorsión posible de la misma garantizando así tener cero triángulos, y todos los elementos utilizados son elementos Shell 2-D CQUAD4, logrando un JACOBIAN CHECK = 0.534, bien por debajo de 0.6.
        Haz <clic> en las imágenes para verlas al completo en su tamaño real

Modos de Vibración (SOL103)

Mediante un Análisis Modal con Simcenter Nastran (SOL103) calculamos la frecuencia fundamental de resonancia de valor 78.6 Hz vibrando a flexión en la dirección del eje Z, con una suma de la masa modal del 54.5% para el primer modo de vibración. Extrayendo los 35 primeros modos de vibración se captura una suma de masa modal por encima del 85% en las tres direcciones X, Y & Z, asegurando así que los resultados de respuesta dinámica en el dominio de la frecuencia sean razonablemente exactos.

Cálculo Estático Lineal (SOL101)

La pieza HINGE se somete a una aceleración de 1G en la dirección del eje Z y se dese conocer la deformada y tensiones bajo el efecto del peso propio: la máxima tensión está por debajo de los 5 MPa, muy por debajo del límite elástico del material S355JR. El desplazamiento máximo resultante tiene un valor de 0.07 mm.
La razón de incluir un análisis estático lineal de AZ=1G es para comparar resultados con los análisis dinámicos aplicando una excitación de AZ=1G mediante una excitación senoidal y RANDOM, ya veréis qué diferencia!!.

Respuesta en Frecuencias (SOL111)

Vamos a ejecutar el análisis dinámico de barrido en frecuencia (SOL111) aplicando una aceleración AZ=1G constante en el rango de frecuencia.

Definiremos una Tabla de Frecuencias incluyendo los puntos exactos de las frecuencias de resonancia en el rango de frecuencia entre 5 y 700 Hz, usando un incremento de frecuencia de 5 Hz en general y de 2.5 Hz localmente alrededor de las frecuencias de resonancia obtenidas inicialmente mediante el análisis de vibraciones (SOL103).

Aplicaremos un amortiguamiento crítico del 10% constante en el rango de frecuencia para obtener los resultados de máxima respuesta en desplazamiento, aceleración y tensión de la pieza y tener así una referencia para comparar con los resultados que obtendremos más adelante con el análisis de vibraciones aleatorias (RANDOM Vibration):

• El máximo desplazamiento tiene un valor TZ=0.33 mm, y es coincidente con la frecuencia fundamental de resonancia a 78.6 Hz.
• La máxima aceleración AZ= 81335 mm/s2, coincidente con la frecuencia de resonancia a 78.6 Hz, por tanto la amplificación dinámica DAF = 81335/10e3 = 8.1 veces mayor.
• La máxima tensión de vonMises = 20 MPa, también coincidente con la frecuencia de resonancia de la pieza, 5x veces mayor que la obtenida mediante un análisis estático lineal (SOL101).

RANDOM VIBRATION

Usando el método modal vamos a determinar la respuesta RANDOM de la pieza HINGE excitada en la dirección del eje Z por una densidad espectral de aceleración (ASD) en unidades G^2/Hz, usando un amortiguamiento crítico del 10% constante en el rango de frecuencia.

Ojo!, al definir un PSD en unidades G^2/Hz provoca que todos los resultados sean en G, incluidas las tensiones. Para que en un Análisis Random las unidades de salida de resultados de respuesta dinámica en tensión sean en MPa, los desplazamientos en mm y la aceleración en mm/s^2 tenemos dos opciones:

• OPCIÓN#1: Modificar la Carga de Aceleración: La función PSD la dejamos en unidades G^2/Hz, pero la carga de aceleración aplicada en el nodo de la base la metemos como 1g = 10e3 mm/s^2, de esta forma todos los resultados del análisis random serán en mm, MPa y mm/s^2.
• OPCIÓN#2: Modificar la función PSD: escalar la función PSD definida originalmente en G^2/Hz para que quede definida en unidades consistentes, en vez de G. Multiplicamos los valores de la función en el eje Y por la aceleración de la gravedad al cuadrado (10e3)^2 = 1e8, convirtiendo la función PSD en unidades (mm/s^2)^2/Hz, y todos los resultados del análisis random serán en unidades mm, MPa y mm/s^2. Claro está, la carga de aceleración que apliquemos al nodo de la base en la dirección de la excitación deberá tener un valor unitario de 1.0 mm/s^2.

Escalar la carga o escalar la función PSD produce los mismos resultados de salida, pero en general escalar la función PSD es lo más habitual.

Vamos a seguir la OPCIÓN#2 escalando la función PSD a unidades (mm/s^2)^2/Hz, así tendremos la función ya preparada para poder compararla directamente con la salida en aceleración en el nodo de la base (superponiendo la gráfica de la excitación de aceleración en la entrada con la respuesta de aceleración en la salida, de forma directa):

La Tabla de Frecuencias es la misma que se ha utilizado para correr el análisis de Respuesta en Frecuencias (SOL111), incluyendo los puntos exactos de las frecuencias de resonancia en el rango de frecuencia entre 5 y 700 Hz, usando un incremento de frecuencia de 5 Hz en general y de 2.5 Hz localmente alrededor de las frecuencias de resonancia obtenidas inicialmente mediante el análisis de vibraciones (SOL103).

Vamos a ajustarla para que empiece a los 20 Hz, coincidiendo con el rango de frecuencia de la excitación Random PSD.

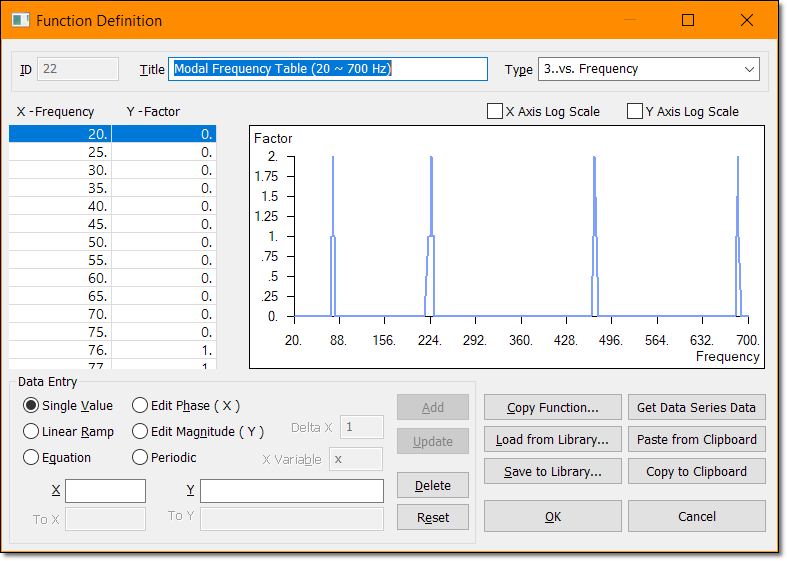
Asimismo definimos la función del amortiguamiento crítico del 10% constante en el rango de frecuencia:

En el nodo de la base (el nodo independiente del RBE2 que está empotrado) se aplica la aceleración unitaria de valor AZ = 1 mm/s2. Nótese que las unidades de la función de Densidad Espectral de Potencia (ASD) son (mm/s^2)^2/Hz, por tanto metiendo la carga de aceleración en valor unitario nos permitirá obtener la respuesta de desplazamientos en mm, la aceleración en mm/s2 y las tensiones en MPa (alternativamente se puede dejar la función ASD en unidades G^2/Hz y aplicar una carga de aceleración de la base en la dirección de la excitación de valor 1g=10e3 mm/s^2, el resultado final es el mismo, da igual modificar la función que modificar la carga).

La carga de aceleración está asociada a una función de amplitud unitaria, constante en el rango de frecuencia (da lo mismo definir el rango de frecuencia entre 0 ~ 100 Hz que entre 0 ~ 1000 Hz, el solver Simcenter Nastran extiende la pendiente de la función según sea necesario):

Aquí está el detalle de la carga aplicada en el SPIDER RBE2 de la base: la aceleración de 1G se aplica en un nodo empotrado!!. No pasa nada, Simcenter Nastran sabe cómo tratar correctamente este dato, OK?.

Parámetros del Análisis Random

Seleccionamos el solver Simcenter Nastran y el tipo de análisis RANDOM RESPONSE:

Pulsamos NEXT hasta llegar a la sección NASTRAN Modal Analysis donde seleccionamos el Método Modal (Ojo!!, un detalle muy importante: por defecto está activo el método directo que es el que usaríamos para definir un análisis SOL108, en vez del método modal que es el que usamos habitualmente para definir un SOL111) y el número de modos que vamos a utilizar para el cálculo RANDOM: para garantizar una buena precisión de los resultados se recomienda seleccionar tantos modos como sean necesarios para obtener una suma de masa modal del 85% en la dirección de la excitación; esta tarea la realizamos antes, cuando preparamos el análisis modal (SOL103).

Pulsamos NEXT para llegar a la sección NASTRAN Dynamic Analysis donde seleccionamos la función de Amortiguamiento Modal y la Tabla de Frecuencias creada anteriormente:

Pulsamos NEXT hasta llegar a la siguiente pantalla: mi recomendación es responder NONE a la petición de generar OUTPUT SETS con resultados nodales y elementales para cada punto de frecuencia incluido en la Tabla de Frecuencias, a mí lo que me interesa es únicamente los Output Sets RMS VALUES y POSITIVE CROSSING, nada más.

Si seleccionas ALL entonces Simcenter Nastran escribirá en el fichero binario de resultados *.op2 un OUTPUT SET por cada punto de frecuencia incluido en la Tabla de Frecuencias con los valores CMRS (Cumulative Root Mean Square) y las funciones PSDF (Power Spectral Density Functions), así como un Output Set de resumen llamado RMS VALUES con desplazamientos, aceleración y tensiones en valores RMS, y el Output Set POSITIVE CROSSING con el valor de la frecuencia aparente (o dominante) de las respuestas anteriores en Hz (o ciclos/segundo) que usaremos para calcular la vida a fatiga del componente.

Pulsamos NEXT y veremos una pantalla donde podemos seleccionar los resultados en nodos y elementos para que Simcenter Nastran genere funciones vs frecuencia que se cargarán automáticamente en FEMAP tras ejecutar el análisis RANDOM.

• Si seleccionamos alguna casilla para generar automáticamente la función de respuesta en nodos o elementos entonces es obligatorio tener creado previamente el grupo de nodos y elementos en los cuales quieras generar funciones de respuesta vs. frecuencia, de lo contrario tendrás que cancelar la orden.
• Si no seleccionas nada, entonces FEMAP no te pedirá ningún grupo.
• En mi caso he activado varias casillas para que se generen respuestas nodales en desplazamiento y aceleración en la dirección del eje Z, así como tensiones elementales SigmaX, SigmaY & TauXY
• Y he creado un grupo incluyendo el nodo#1 donde se aplica la excitación de la base y el nodo#262 situado en la posición más alejada de la pieza donde el desplazamiento y aceleración serán máximos, así como el elemento#4 donde se esperan las máximas tensiones.

Pulsamos NEXT y por fin llegamos a la ventana más importante de un análisis Random: aquí es donde seleccionamos la función PSD correcta en unidades (mm/s^2)^2/Hz, el factor de correlación (por defecto 1.0) y el método de interpolación (logarítmico por defecto). En este ejemplo tenemos un único PSD, pero puede darse el caso de tener múltiples PSD independientes excitando diferentes posiciones, por ejemplo, las cuatro ruedas de un camión pueden estar excitadas por diferentes PSD por la rugosidad de la carretera; para poder activarlos hay que definir diferentes SUBCASES y crear diferentes tablas de correlación.

Pulsamos NEXT y definimos el set de restricciones y el set de cargas:

Y pulsando NEXT finalmente llegamos a la definición del NASTRAN Output Request donde seleccionamos los resultados que queremos obtener tras ejecutar el análisis Random: en este caso desplazamiento, aceleración y tensiones.

Si hacemos un PREVIEW ANALYSIS podremos ver el fichero de entrada de Simcenter Nastran con la definición de los parámetros del análisis Random:

Resultados del Análisis Random

Tras ejecutar el Análisis Random y cargar automáticamente los resultados en FEMAP nos pregunta si queremos leer las funciones PSD y los resultados de tensiones con el CORNER DATA además del centro del elemento. Respondemos a todo con YES:

Y en FEMAP se crean las siguientes carpetas de resultados con tres Output Sets:

• X-Y Plot Summary: un resumen de todos los resultados (output vectors).
• Positive Crossing: es la frecuencia aparente (o dominante) de todos los output vectors, en Hz (es decir, ciclos/segundo). Este valor lo usaremos para calcular “a mano” la vida a fatiga del componente usando la Regla de Palmgren-Miner de daño acumulado.
• RMS Values: valores RMS de todos los output vectors.

Resultados RMS

Podemos comprobar que las tensiones RMS de un análisis Random son significativamente mayores que las obtenidas a partir de un análisis harmónico senoidal de barrido en frecuencias (SOL111): pasamos de una tensión de 20 MPa del análisis de barrido en frecuencia a cerca de 100 MPa de un análisis Random, casi 5x veces mayor!!.

La siguiente imagen muestra el reparto de las tensiones elementales de vonMises representadas en el “Element Centroid” (es decir, en el centro del elemento) que como podéis comprobar son en general siempre menores que las tensiones nodales.

Podemos representar en el CHARTING de FEMAP las funciones generadas automáticamente durante el Análisis Random de las componentes de tensión RMS elementales SigmaX, SigmaY, SigmaXY (lastima que la opción no incluya las tensiones elementales de vonMises):

Una recomendación muy importante que siempre se debe seguir cuando se realiza un Análisis RANDOM es verificar que la excitación de entrada de aceleración ASD y la respuesta de salida en el nodo de la base están en equilibrio, es como verificar en un análisis estático lineal (SOL101) que el equilibrio entre fuerzas y reacciones está satisfecho, de lo contrario los resultados son todo menos correctos. Pues bien, como la función de entrada PSD ya la hemos escalado en unidades (mm/s^2)^2/Hz coherentes con las unidades de aceleración de la salida, directamente hacemos la comparativa entre el PSD de entrada y la respuesta de salida ACCELZ en el nodo#1 de la base: parece que en algunos tramos las curvas no son totalmente coincidentes, ¿Cuál podrá ser la razón?.

Pues es un problema provocado por el formato lineal de los resultados: si representamos los ejes X e Y en formato logarítmico veremos una exactitud total entre el ASD de entrada y la aceleración de salida en el nodo#1 de la base, mayor precisión imposible!!:

También es interesante representar la respuesta dinámica en aceleración en el nodo#262 que es el nodo más solicitado de la pieza junto con la excitación ASD de entrada aplicada en el nodo#1 de la base, todo en la misma gráfica X-Y, directamente ya en formato logarítmico: la amplificación dinámica es del orden de 66.1 veces!!.

Positive Crossings

Esto es un análisis de vibraciones, así que la vida a fatiga del componente nos interesa mucho: vamos a utilizar el resultado POSITIVE CROSINGS que es un valor en Hz (ciclos/segundo) que nos permitirá calcular la suma de daño a fatiga basándonos en la duración de la excitación.

La siguiente imagen muestra el resultado POSITIVE CROSSINGS = 82 Hz (valor cercano a la frecuencia fundamental de resonancia de la pieza) que se produce en el elemento más solicitado con una tensión máxima de vonMises de unos 100 MPa. Pues bien, esto significa que bajo el PSD de excitación de ruido blanco la pieza sufre una tensión alterna de unos 100 MPa a una frecuencia de 82 Hz.

• Estadísticamente hablando, esta tensión de 100 MPa representa el valor 1σ que sufrirá el 68.3% del tiempo.
• Un valor 2σ = 2*100 = 200 MPa lo sufrirá el 95.4 – 68.3 = 27.1% del tiempo.
• Un valor 3σ = 3*100 = 300 MPa lo sufrirá el 99.7 – 95.4 = 4.3% del tiempo.
• Esto representa un total del 99.7% de las tensiones que sufrirá la pieza HINGE.
• Es probable que la pieza HINGE vea tensiones 4σ y superiores, pero esto sólo pasará el 100 – 99.7 = 0.3% del tiempo, por tanto podemos ignorarlo perfectamente.

Cálculo a Fatiga

Utilizaremos la Suma de Daño Acumulado de Palmgren-Miner para calcular cuántos ciclos de vida resistirá el componente HINGE bajo este nivel de tensiones 1σ, 2σ y 3σ hasta que la pieza falle.

La Regla de Miner de daño acumulativo viene dada por la siguiente ecuación:

• En primer lugar generamos en el software de Análisis de Fatiga winLIFE una curva S-N para un material S335JR usando parámetros razonables de forma de trabajo, tamaño, acabado superficial, etc..  modificativos del límite de fatiga de la probeta rotatoria, obteniendo la siguiente curva S-N de la pieza con una límite de fatiga σe=150 MPa.
• Con los valores de tensión alterna de 100, 200 y 300 MPa entramos en la curva S-N y obtenemos el nº de ciclos para el fallo:
  • Para una tensión alterna 1σ=100 MPa que experimenta el 68.3% del tiempo la pieza tiene vida infinita, la tensión está bien por debajo del límite de fatiga de la pieza.
  • Para una tensión alterna 2σ=200 MPa que experimenta el 27.1% del tiempo el nº de ciclos para el fallo es de 2.35e5 ciclos.
  • Para una tensión alterna 3σ=300 MPa que experimenta el 4.3% del tiempo el nº de ciclos para el fallo es de 3.1e4 ciclos.

Los resultados anteriores se substituyen en la Ecuación de Miner para calcular cuántos ciclos puede soportar la pieza HINGE hasta alcanzar el fallo por fatiga del material cuando la suma de daño es igual a DAMAGE SUM = 1.0:

Despejando n en la ecuación anterior obtenemos una Vida a Fatiga n = 3.92E5 ciclos.

Si la parte más solicitada de la pieza vibra a una frecuencia Positive Crossings = 82 Hz = 82 ciclos/s, entonces la pieza fallará en un tiempo t = 3.92e5/82 = 4780 segundos = 1.33 horas para el fallo.

Conclusión

Mientras la pieza HINGE no se exponga a una vibración por ruido blanco mayor de 1.33 horas, la pieza no se romperá.

–oo§oo–

 Enlaces de Descarga Interesantes

• PSD-Random-Vibration-tutorial-for-Simcenter-Femap-and-Nastran (Predictive Engineering/USA)
• PSD-Random-Vibration-Tutorial-Part-II-Application (Predictive Engineering/USA)
• Dynamic-Analysis-User-Guide-for-Simcenter-FEMAP-and-Nastran (Predictive Engineering/USA)
• Simcenter-Nastran-Basic-Dynamics-User-Guide-V2020_2 (SIEMENS PLM)
• Simcenter-Nastran-Advanced-Dynamics-User-Guide-V2020_2 (SIEMENS PLM)
• Para saber más sobre RANDOM ANALYSIS visitad la web de la NASA: https://femci.gsfc.nasa.gov/random/

Espero que este artículo sobre el Análisis RANDOM con Simcenter FEMAP y NASTRAN os resulte útil e interesante, como veis es un tema apasionante pero a la vez muy complejo, recomiendo leer con atención los manuales de Simcenter Nastran Básico y Avanzado, es la biblia y allí están las respuestas a casi todas las preguntas que podamos tener; y el material de PREDICTIVE ENGINEERING (USA) es fundamental, pone en práctica el análisis dinámico haciendo fácil lo difícil!!; y la referencia a la web de la NASA muy interesante, no dejéis de visitarla!!.
En fin, cualquier pregunta que tengáis no dudéis en consultarme, si conozco la respuesta encantado de ayudaros – Gracias!.

Saludos,
Blas.